Newsletter: Hurst Exponent Applications, From Regime Analysis to Arbitrage
Hurst exponent is used for market timing and uncovering statistical arbitrage opportunities
Hello,
Thank you for subscribing to my newsletter. To ensure you receive this newsletter in your inbox, please add us to your safe senders list.
One of my favourite ways to characterize the market regime is by using the Hurst exponent. However, its applications are not limited to identifying market regimes. There are innovative ways to utilize it. In this newsletter, I will discuss two approaches to applying the Hurst exponent.
Using the Hurst Exponent to Time the Market
The Hurst exponent can be employed to directly time the market. Reference [1] calculated the moving Hurst exponents for rolling windows of 100 and 150 days. The timing signals are subsequently generated by using these calculations.
Findings
-The study suggests that the Moving Hurst (MH) indicator is effective for forecasting and managing volatility in Indian equity markets.
-MH is more effective at capturing profitable trading opportunities than Moving Averages (MA).
-MH is a less lagging indicator than MA, making it more responsive to market changes.
-MH incorporates principles from chaos theory and fractal analysis, offering a unique perspective for market analysis.
-The research was conducted in the Indian stock market. However, it can be readily applied to any stock market.
Reference
[1] Shah, Param, Ankush Raje, and Jigarkumar Shah, Patterns in the Chaos: The Moving Hurst Indicator and Its Role in Indian Market Volatility. Journal of Risk and Financial Management 17: 390, 2024
Using the Hurst Exponent for Pairs Trading
The Hurst method isn’t restricted to single underlying assets; it can also be applied to a pair of stocks to identify pairs trading (statistical arbitrage) opportunities. Reference [2] proposed a new approach to measure the co-movement of two price series through the Hurst exponent of the product.
Findings
- The Hurst exponent of the product series, referred to as HP, can measure the existence of a relationship between two series.
- The HP method is a new way to measure the dependence between two series, detecting various types of relationships, including correlation, cointegration, and non-linear relationships, even when the relationship is weak or given by a copula.
- This method is particularly useful for studying financial series as it gives more weight to high increments than low increments, unlike other correlation measures.
- The efficiency of the HP method was tested through a statistical arbitrage technique for pairs selection and compared with the classical correlation method. Results indicate that the HP method performs better in most cases.
Reference
[2] José Pedro Ramos-Requena, Juan Evangelista Trinidad-Segovia, and Miguel Ángel Sánchez-Granero, An Alternative Approach to Measure Co-Movement between Two Time Series, Mathematics 2020, 8, 261
Educational Video
This seminar by Markis Vogl presents the theory and application of the Hurst exponent.
Abstract
My presentations elaborates on the meaning of Hurst exponents, namely, that instead of long memory, fractal trends are measured instead (contradicting Mandelbrot's conception). Further, the talk encompasses the generation of rolling window (time varying) Hurst exponent series based upon the cascadic level 12 wavelet filtered (denoised) S&P500 logarithmic return series (2000-2020). The Hurst exponent series are then analysed with a generalizable nonlinear analysis framework, which allows the determination of the underlying empirical data generating process.
Volatility Weekly Recap
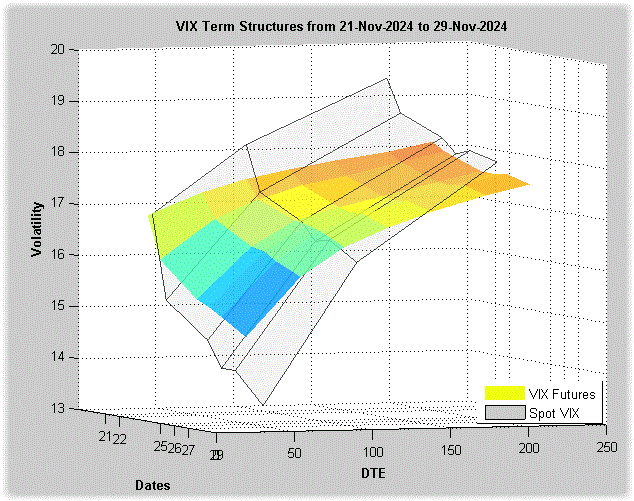
Last week was a shortened trading week due to the Thanksgiving holiday, and the market remained quiet. The figure below shows the term structures for the VIX futures (in green and yellow) and the spot VIX (in grey).
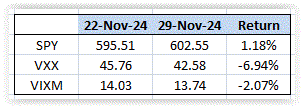
We can observe that the short-term VIX futures were in contango and declined toward the end of the week, while mid-term futures remained relatively flat. This dynamic resulted in returns of -6.94% for VXX and -2.07% for VIXM.
Around the Quantosphere
Below are some interesting links from the quant world:
-Hedge Fund Fermat Says Returns Took a Hit Amid Catastrophe Bond Selloff (insurancejournal.com)
- No-arbitrage Model for Pricing CAT Bonds (linkedin.com)
- Quant of the year: Julien Guyon (risk.net)
- QVR targets JPMorgan’s options-selling behemoth (hedgeweek.com)
Thank you for reading and let me know your thoughts in the comments below or by replying to this email!
Disclaimer
This newsletter is not investment advice. It is provided solely for entertainment and educational purposes. Always consult a financial professional before making any investment decisions.